Radiometric dating is a means of determining the "age" of a mineral specimen by determining the relative amounts present of certain radioactive elements. By "age" we mean the elapsed time from when the mineral specimen was formed.
Radioactive elements "decay" (that is, change into other elements) by "half lives." If a half life is equal to one year, then one half of the radioactive element will have decayed in the first year after the mineral was formed; one half of the remainder will decay in the next year (leaving one-fourth remaining), and so forth. The formula for the fraction remaining is one-half raised to the power given by the number of years divided by the half-life (in other words raised to a power equal to the number of half-lives).
If we knew the fraction of a radioactive element still remaining in a mineral, it would be a simple matter to calculate its age by the formula
log F = (N/H)log(1/2)
where: F = fraction remaining
N = number of years
and H = half life.
To determine the fraction still remaining, we must know both the amount now present and also the amount present when the mineral was formed. Contrary to creationist claims, it is possible to make that determination, as the following will explain:
By way of background, all atoms of a given element have the same number of protons in the nucleus; however, the number of neutrons in the nucleus can vary. An atom with the same number of protons in the nucleus but a different number of neutrons is called an isotope. For example, uranium-238 is an isotope of uranium-235, because it has 3 more neutrons in the nucleus. It has the same number of protons, otherwise it wouldn't be uranium. The number of protons in the nucleus of an atom is called its atomic number. The sum of protons plus neutrons is the mass number.
We designate a specific group of atoms by using the term "nuclide." A nuclide refers to a group of atoms with specified atomic number and mass number.
Potassium-Argon dating:
The element potassium (symbol K) has three nuclides, K39, K40, and K41.
Only K40 is radioactive; the other two are stable. K40 can decay in two
different ways: it can break down into either calcium or argon. The
ratio of calcium formed to argon formed is fixed and known. Therefore
the amount of argon formed provides a direct measurement of the amount
of potassium-40 present in the specimen when it was originally formed.
Because argon is an inert gas, it is not possible that it might have been in the mineral when it was first formed from molten magma. Any argon present in a mineral containing potassium-40 must have been formed as the result of radioactive decay. F, the fraction of K40 remaining, is equal to the amount of potassium-40 in the sample, divided by the sum of potassium-40 in the sample plus the calculated amount of potassium required to produce the amount of argon found. The age can then be calculated from equation (1).
In spite of the fact that it is a gas, the argon is trapped in the mineral and can't escape. (Creationists claim that argon escape renders age determinations invalid. However, any escaping argon gas would lead to a determined age younger, not older, than actual. The creationist "argon escape" theory does not support their young earth model.)
The argon age determination of the mineral can be confirmed by measuring the loss of potassium. In old rocks, there will be less potassium present than was required to form the mineral, because some of it has been transmuted to argon. The decrease in the amount of potassium required to form the original mineral has consistently confirmed the age as determined by the amount of argon formed.
Carbon-14 dating:
See Carbon 14 Dating in this web site.
Rubidium-Strontium dating:
The nuclide rubidium-87 decays, with a half life of 48.8 billion years,
to strontium-87. Strontium-87 is a stable element; it does not undergo
further radioactive decay. (Do not confuse with the highly radioactive
isotope, strontium-90.)
Strontium occurs naturally as a mixture of several
nuclides, including the stable isotope strontium-86. If three different
strontium-containing minerals
form at the same time in the same magma, each strontium containing
mineral will have the same ratios of the different strontium nuclides,
since all strontium nuclides behave the same chemically. (Note that
this does not mean that the ratios are the same everywhere on earth. It
merely means that the ratios are the same in the particular magma from
which the test sample was later taken.) As strontium-87 forms, its ratio
to strontium-86 will increase. Strontium-86 is a stable element that does
not undergo radioactive change. In addition, it is not formed as the result
of a radioactive decay process. The amount of strontium-86 in a
given mineral sample will not change. Therefore the relative amounts of
rubidium-87 and strontium-87 can be determined by expressing their ratios
to strontium-86: Rb-87/Sr-86 and Sr87/Sr-86 We measure the amounts of rubidium-87 and
strontium-87 as ratios to an unchanging content of strontium-86.
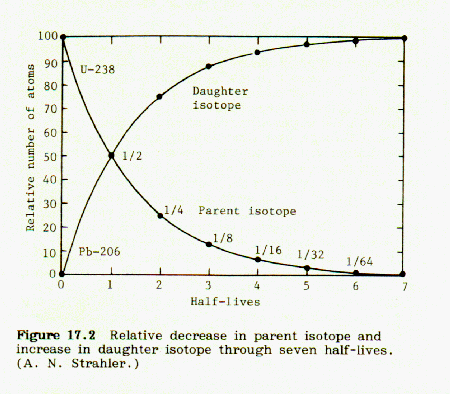
Because of radioactivity, the fraction of rubidium-87 decreases from an initial value of 100% at the time of formation of the mineral, and approaches zero with increasing number of half lives. At the same time, the fraction of strontium-87 formed increases from zero and approaches 100% with increasing number of half-lives. The two curves cross each other at half life = 1.00. At this point the fraction of Rb87 = Sr87 = 0.500. At half life = 2.00, Rb87 = 25% and Sr87 = 75%, and so on.
These curves are illustrated in Fig 17.2, p. 131, Strahler, Science and Earth History:

Points are taken from these curves and a plot of fraction Sr-87/Sr-86 (as ordinate) vs. Rb-87/Sr-86 (as abscissa) is made. It turns out to be a straight line with a slope of -1.00. The corresponding half lives for each plotted point are marked on the line and identified.
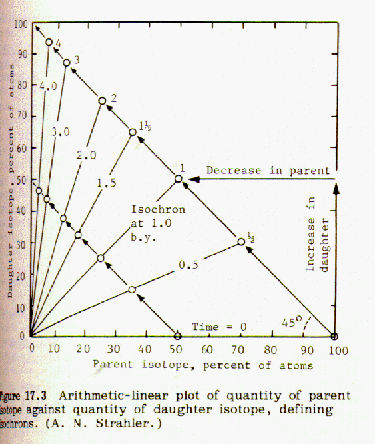
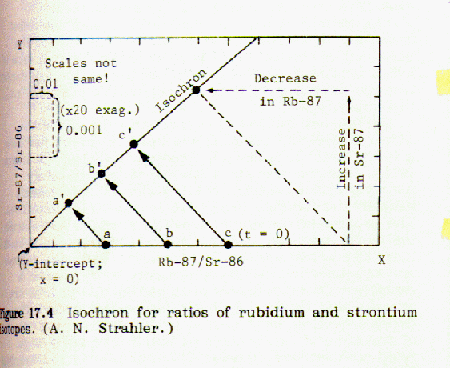
When the fraction of rubidium-87 is plotted against the fraction of strontium-87 for a number of different minerals from the same magma an isochron is obtained. If the points lie on a straight line, this indicates that the data is consistent and probably accurate. An example of this can be found in Strahler, Fig 17.5, page 133:

If the strontium-87 isotope was not present in the mineral at the time it was formed from the molten magma, then the geometry of the plotted isochron lines requires that they all intersect the origin, as shown in figure 17.3. However, if strontium 87 was present in the mineral when it was first formed from molten magma, that amount will be shown by an intercept of the isochron lines on the y-axis, as shown in Fig 17.5 above. Thus it is possible to correct for strontium-87 initially present.
Comparing figures 17.2 and 17.3, it is obvious that the steeper the
slope of the isochron line, the greater the number of half lives, and
the older the sample. The age of the sample can be obtained by
choosing the origin at the y intercept. In Fig 17.5 the
isochron line has a slope of 0.005/0.105 = 0.048 and intersects the Sr87 axis
at 0.699 = y intercept.
Note that the amounts of rubidium 87 and strontium 87 are
given as ratios to an inert isotope, strontium 86. However, in calculating
the ratio of Rb87 to Sr87, we can use a simple analytical geometry solution
to the plotted data.
Again referring to Fig. 17.3,
the slope of the strontium-87/rubidium-87 line is -1, and y = 1-x.
Therefore, with the origin placed at the y intercept, the intersection
of the Rb/Sr line and the isochron line can be obtained by solving
the equation 1-x = 0.048x, giving the result x = 0.954, which is
the rubidium-87/strontium-86 ratio corresponding to the given
isochron line.(The corresponding strontium-87/strontium-86 ratio
is 1.000 - 0.954 = 0.046) Thus the fraction of Rb87 decayed is 0.954.
Since the half-life of Rb87 is 48.8 billion years,
we can substitute in the half-life equation: 0.954 = (1/2) raised to the
power (age/48.8), where age = age in billions of years.
Therefore:
log(.954) = (age/48.8)(log 1/2).
This solves to
age = 3.3 billion years.
When properly carried out, radioactive dating test procedures have shown consistent and close agreement among the various methods. If the same result is obtained sample after sample, using different test procedures based on different decay sequences, and carried out by different laboratories, that is a pretty good indication that the age determinations are accurate. Of course, test procedures, like anything else, can be screwed up. Samples can be contaminated and/or improperly prepared. Mistakes can be made at the time a procedure is first being developed. Creationists seize upon any isolated reports of improperly run tests and try to categorize them as representing general shortcomings of the test procedure. This like saying if my watch isn't running, then all watches are useless for keeping time.
Creationists also attack radioactive dating with the argument that half-lives were different in the past than they are at present. There is no more reason to believe that than to believe that at some time in the past iron did not rust and wood did not burn. Furthermore, astronomical data show that radioactive half-lives in elements in stars billions of light years away is the same as presently measured.
On pages 358 and 359 of The Genesis Flood, creationist authors Whitcomb and Morris present an argument to try to convince the reader that ages of mineral specimens determined by radioactivity measurements are much greater than the "true" (i.e. Biblical) ages. The mathematical procedures employed are totally inconsistent with reality. Henry Morris has a PhD in Hydraulic Engineering, so it would seem that he would know better than to author such nonsense. Apparently, he did know better, because he qualifies the exposition in a footnote stating:
This discussion is not meant to be an exact exposition of radiogenic age computation; the relation is mathematically more complicated than the direct proportion assumed for the illustration. Nevertheless, the principles described are substantially applicable to the actual relationship.
Morris states that the production rate of an element formed by radioactive decay is constant with time. This is not true, although for a short period of time (compared to the length of the half life) the change in production rate may be very small. Radioactive elements decay by half-lives. At the end of the first half life, only half of the radioactive element remains, and therefore the production rate of the element formed by radioactive decay will be only half of what it was at the beginning.
The authors state on p. 358:
If these elements existed also as the result of direct creation, it is reasonable to assume that they existed in these same proportions. Say, then, that their initial amounts are represented by quantities of A and cA respectively. [c being the ratio of the initial amounts of the two elements at the moment of "creation."] Now if at some time the incidence of environmental radiation is increased, both [decay] rates will be increased in roughly these same proportions; assume that both are multiplied by a factor k and that the increased rates persist throughout a length of time T'. Prior to this time the normal rates applied and persisted, say, for a time To, and following this period they applied again for a
time of T*.
Morris makes a number of unsupported assumptions:
(1) His basic equation states that the amount of a daughter element
formed = A + R(T), where A = amount existing at the "moment
of creation," T = time from
creation, and R is an unchanging rate of formation.
An unchanging value of R requires that the rate of decay is
constant with time, meaning that if, for example,
1% of the element decays in a year's time, at the end of a hundred
years it will be all gone. This is not correct; radioactive elements
decay by half lives, as explained in the first paragraphs of
this post.
(2)He stated that "Environmental radiation" can change the rate of
decay of radioactive elements. There is absolutely no evidence to support
this assumption, and a great deal of evidence that electromagnetic
radiation does not affect the rate of decay of terrestrial radioactive
elements.
(3)He postulates that the environmental radiation would spontaneously
manifest itself, and at a later time, spontaneously disappear.
(4)He assumes that the environmental radiation would penetrate the
earth's crust, with no diminution in intensity, and affect all radioactive
elements in the same way and to the same degree, but without affecting any
living things that might be present.
He sums it up with the equations:
A + R(To) + k(R)(T') + R(T*) = Quantity of first element, and
cA + cR(To) + k(cR)(T') + cR(T*) = Quantity of second element.
He then calculates an "age" for the first element by dividing its
quantity by its decay rate, R; and an "age" for the second element
by dividing its quantity by its decay rate, cR. It's obvious from the
above two equations that the result shows the same age for both
elements, which is:
A/R + To + k(T') + T*. Since
the actual age would necessarily be
To + T' + T*,
Morris concludes that the age determined by radioactive measurements
is necessarily greater than the true age.
Of course, the mathematics are completely wrong. The correct relation
can obtained by rearranging the equation given
at the beginning of this post: the number of years N corresponding
to a rate of
decay (properly expressed as the half-life = H) is:
For a half life of 1000 years, the following table shows the fraction remaining for various time periods:
Fraction remaining: 0.9 0.7 0.6 0.5 0.3 0.1
Corresponding number of years: 152 514 737 1000 1737 3322
By way of contrast, the following table displays the incorrect values calculated on the basis of the Morris straight line relationship: amount = A + R(T)
Morris identifies the rate of daughter element production as R, with no reference to the effect of the amount of parent element on the rate R. In all his mathematics, R is taken as a constant value. We may therefore set R as equal to the initial rate in the above table:
Calculating, using the Morris equation: amount formed = R(T), the amount of element (expressed as a fraction of the amount of the parent element) formed for the same time periods in the above table is:
Number of years: 152 514 737 1000 1737 3322
Fraction formed: 0.1 0.34 0.48 0.66 1.14 2.18
Fraction remaining: 0.9 0.66 0.52 0.34 (-)0.14 (-)1.18
Morris' equations would indicate that after 1520 years the amount of parent element would be completely gone, but the daughter element would nevertheless continue to be formed!
Click on the web site of Dr. Roger Wiens of Cal Tech for a detailed analysis of the accuracy of radioactive dating.
Additional information is also available in talk.origins faqs: Isochron Dating and Age of Earth