Charles Thaxton, Walter Bradley, and Roger Olsen have written a book The Mystery of Life's Origin: Reassessing Current Theories. The book was prepared in conjunction with the publishing program of the Foundation for Thought and Ethics, P.O. Box 830721, Richardson, TX 75083-0271, Phone (214) 661-1661, FAX: (214) 661-2989. It was published by Lewis and Stanley, 13612 Midway Rd., Suite 500, Dallas, Texas 75244. Thaxton was academic editor of the creationist text Of Pandas and People.

This review covers the thermodynamics claims in chapters 7, 8, and 9 of MOLO. These chapters are presented on the MoLO web site http://shell3.ba.best.com/~dolphin/mystery/.

The book is sub titled Reassessing Current Theories. The title implies that the authors believe that presently accepted theories regarding evolutionary science have serious shortcomings. However, there is nothing in Chapter 7 to support this contention. Chapter 7, while technically correct, fails in the difficult task of satisfactorily explaining to the lay person the relation between entropy, probability, and the thermodynamics of living systems. It lists numerous references which in general are obtainable only in university libraries and in addition are very difficult for the lay person to understand. The reader is left with the impression, whether true or not, that the authors' approach is more authoritarian than explanatory.

They stress that entropy change results from energy flow, in spite of the fact that a spontaneous entropy change can occur even when no heat flow at all occurs.

The authors state that the probability of thermodynamics change is dictated by the probability of "energy rich" configurations going to "energy poor" configurations, resulting in an increase in entropy. This conclusion is presented using their model of entropy change described as only due to heat flow. This is true in the case of reversible heat flow, but the irreversible case is covered by the use of the greater than or equal sign, as used in their equation 7-9. The significance of the effect of the change in Gibbs free energy is often not mentioned, leading to a discontinuity in the logical development of the mathematical relationships.

Discussion of Mathematics of Chapter 7

In order to understand the mathematical procedures employed by the authors, it is essential to first review the some of the basic mathematics of thermodynamics.

Most thermodynamic equations represent a change in the properties of a system when it is changed in some manner. Some examples of change are: (1) A chemical reaction between two interacting systems, as hydrogen and oxygen combining to form water; (2) Absorption of heat by a system, as when heat flows into a house during the summer; (3) Absorption of work by a system, as when air is pumped into a tank; (4) Work done by a system, as when air under pressure runs an air motor. When these kinds of changes take place, there is change in the properties of the system. A mixture of two gases becomes a liquid; the temperature of the house interior rises; the density and pressure of the air changes. Changes in properties of a system are indicated mathematically by the Greek letter capital delta: . The symbol indicates an increase or decrease of the quantity immediately following.

Internal energy is a property of a system, and a change in internal energy is denoted as E:

       E = q - w        (1)

       S = q/T          (2)

Therefore: E = TS - w    (3)

Where: w = work done by the system
       q = heat absorbed by the system
       E = energy content of the system
       S = entropy content of the system
       T = absolute temperature

Equation (2) represents the fundamental definition of entropy. Entropy is a "state function", that is, it depends only on the present condition of the system. In calculating the change of entropy, it is generally necessary to determine the amount of heat q absorbed (or evolved, if there is a decrease in entropy) when the process takes place reversibly. (The definition of reversible and irreversible processes will be explained later.) In some cases the change in entropy accompanying a process will be the same, regardless of whether or not the process is reversible or irreversible. This is the case when there is no work energy that could be transferred as a consequence of the change. An example of this would be the heat transfer when a hot stone is dropped into a bucket of cold water. However, since both E and S are fixed for any specific change in the state of the system, equation (3) is valid only if w represents a fixed value of reversible work energy transfer.

A clear distinction must be made between the entropy change of a system and the overall entropy change of a system and its surroundings. In a reversible process the entropy change in a system due to the action of the surroundings is equal and opposite in sign to the entropy change of the surroundings. Therefore the overall net entropy change is zero. In an irreversible process the entropy change in the surroundings is greater than the entropy change in the system. Therefore the overall net entropy change is greater than zero.

In many cases the entropy change in a system is calculated on a theoretical basis as the entropy change in the surroundings for a reversible process, even though such a process can not actually be carried out experimentally. In other words, the concept of reversibility is a mathematical tool. All real processes are irreversible, although in some cases they may be a very close approximation to reversible processes. The authors do not always make clear the distinction between reversible and irreversible processes. Instead they at times merely use the "greater than or equal" sign (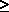), as in their equation 7-9 to cover both reversible and irreversible processes.

Rearranging equation (3):

    
       TS = E + w     (4)

The work done by a system (or sub system) can be a combination of useful work obtained, and work done against atmospheric pressure.

Therefore:

       
       w = PV + w'          (5)

Where: w' = work done that can be utilized for useful purposes, eg
            lifting a weight or pumping a fluid.
       P = atmospheric pressure
       V = volume, and V = change in volume
           accompanying work against atmospheric pressure.  

Combining (4) and (5):

       TS = E + PV + w'    (6)

If the change is brought about in an irreversible manner so that no work, other than PV work, is done, then w' = 0, and:

       
       TS = E + PV      (7)
 

In this case, since q = TS, the heat evolved (or absorbed) is equal to E + PV.
The expression E + PV is called the enthalpy, and is designated by the symbol H. For processes taking place at constant pressure without producing (or absorbing) useful work, H represents the heat evolved or absorbed.

For an enthalpy change at constant pressure:

      
       H = E + PV        (8)

S, E, T, P, and V are properties of a system. Referring again to equation (6), the reversible work w' represents the maximum useful work that can be obtained from a thermodynamic change. This maximum reversible work obtainable is designated by G, the Gibbs free energy. The free energy is a property of the system, like P, V, and T. When work is done, the free energy content of a system is reduced. For the maximum work theoretically possible, w' = -G, and from equation (6):

       TS = E + PV - G    (9)

Rearranging and combining with equation (8):

       G = H - TS        (10)

and:   S = [H - G]/T     (11)

If the process is carried irreversibly so that no work is done, for example combustion in a calorimeter, then:

       

       S = H/T

Here, S represents the change in entropy of the surroundings, not the entropy change of the system. However, the enthalpy change H depends only on the initial and final states, and is the same as in the reversible process. Therefore if S can be determined for a reaction, G can be calculated from S and H.

H/T, the irreversible entropy change determined by combustion in a calorimeter, is entirely different and often of opposite sign than the reversible entropy change obtained from the relation G = H - TS.

NOTE: A positive value (heat absorbed) of H does not mean the reaction can not take place. All that is necessary is that the values conform to the equation G = H - TS.

G can be determined by direct measurement of the emf of a voltaic cell. It can also be calculated from absolute entropy values obtained from measurements of heat capacity versus absolute temperature. The mathematics of thermodynamics permits the calculation of the effect of pressure and temperature on values of S, H and G.

The theoretical maximum potential for useful work is represented by G. When the value of G calculated from equation (10) is negative, the change can occur, although the use of a catalyst may be necessary to make it happen. Note that it is not always necessary for heat to evolve for a change to occur spontaneously. H can be zero or even less than zero.

When H is zero,equation (10) becomes:

       G = -TS       (H = 0)

An example of H equal to zero is the free expansion of a perfect gas. The internal energy of the gas is unchanged on free expansion, and no P-V work is done. In this case there is an entropy change even though there is no energy flow. If the same change takes reversibly, with no heat flow (adiabatic conditions), the work output is equal to G. G is the same in either case, except that in the reversible process it represents the work actually obtained, while in the irreversible free expansion process it represents the work that could have been obtained.

The authors make the statement:

It has often been argued by analogy to water crystallizing to ice that simple monomers may polymerize into complex molecules such as protein and DNA. The analogy is clearly inappropriate, however. The E + PV term (equation 7-9) in the polymerization of important organic molecules is generally positive (5 to 8 kcal/mole), indicating the reaction can never spontaneously occur at or near equilibrium. [Note: If E + PV is positive, the entropy term in eq. 7.9 must be negative due to the negative sign which precedes it. The inequality can only be satisfied by S being sufficiently positive, which implies disordering.]

The authors have previously defined equilibrium as the condition in which the flow of heat is equalized so that there is no temperature differential driving force. Eliminating the time factor, which is irrelevant in thermodynamics, equation (7-9) can be written as:

       S - H/T 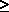 0     (7-9)

Rearranging equation (10):

       S - H/T = - G/T        (11)

S - H/T = 0

By contrast the E + PV term in water changing to ice is a negative, -1.44 kcal/mole, indicating the phase change is spontaneous as long as T = 273 deg. K, as previously noted. The atomic bonding forces draw water molecules into an orderly crystalline array when the thermal agitation (or entropy driving force, TS) is made sufficiently small by lowering the temperature. Organic monomers such a amino acids resist combining at all at any temperature, however, much less in some orderly arrangement.

The statement is misleading in that it does not make clear that the the fundamental expression for the driving force in thermodynamic change is G. The problem here is that the other terms, by themselves, do not provide a reliable basis for the comparison of one reaction to another.

Referring to equation (10):

G = H - TS

At the freezing point the two phases are in equilibrium, and G = 0.

and: H = TS

H = -80 cal/gm  (enthalpy change when water freezes to ice)

TS = 273 x (-.293 entropy units) = -80 cal/gm

Below the freezing point at 270 deg K:

H = -80 cal/gm

TS = 270 x (-.293) = -79 cal/gm

G = H -TS
     = -80 -(-79)
     = -1  and the reaction can proceed.

Above the freezing point at 276 deg K:

H = -80 cal/gm

TS = 276 x (-.293) = -81 cal/gm

G = H - TS
     = -80 -(-81)
     = +1 and the reaction can not proceed

In the section, Closed Systems Far from Equilibrium, the authors treat entropy effects as a manifestation of "entropy flux" due to "energy flow through the system." They define S_e as entropy flux due to energy flow through the system, and S_i as entropy production inside the system. The total entropy change is stated as:

       S = Se + Si      (7-11)

The authors do not provide specific mathematical descriptions of derivations of the terms in the above equation, nor do they provide information on how it could be utilized to determine the free energy of a chemical reaction. With respect to equation (7-11) they state the following:

Where S_e is the entropy flux due to energy flow through the system, and S_i is the entropy production due to irreversible processes such as diffusion, heat conduction, heat production, and chemical reactions. We will note when we discuss open systems in the next section that S_e includes the entropy flux due to mass flow through the system as well.

It would be helpful in understanding Equation (7-11) if the authors would provide some explanation of its derivation. It appears that it is based on the theory that chemical changes in living things can be treated as a flow system:

Energy flow through a system is the equivalent to doing work continuously on the system to maintain it some distance from equilibrium. [snip] An open system offers an additional possibility for ordering-that of maintaining a system far from equilibrium via mass flow through the system, as will be discussed in the next section.

In living plants, the energy flow through the system is supplied principally by solar radiation. In fact, leaves provide relatively large surface areas per unit volume for most plants, allowing them to "capture" the necessary solar energy to maintain themselves far from equilibrium. This solar energy is converted into the necessary useful work (negative S_e in equation 7-11) to maintain the plant in its complex, high-energy configuration by a complicated process called photosynthesis. [snip] A source of energy alone is not sufficient, however, to explain the origin or maintenance of living systems. The additional crucial factor is a means of converting this energy into the necessary useful work to build and maintain the complex living systems from the simple biomonomers that constitute their molecular building blocks.

The authors have failed to provide any mathematical support to give credence to their statements. The title of Chapter 7 is Thermodynamics of Living Systems, but there is nothing specific relating to how thermodynamics is actually applied to obtain specific data. Rather the authors summarize the whole chapter as follows:

In mathematical formalism, these concepts may be summarized as follows:

(1) The second law of thermodynamics requires only that the entropy production due to irreversible processes within the system be greater than zero; i.e.,

       Si > 0      (7-15>

(2) The maintenance of living systems requires that the energy flow through the system be of sufficient magnitude that the negative entropy production rate (i.e., useful work rate) that results be greater than the rate of dissipation that results from irreversible processes going on with the systems; i.e.,

       |Se| > Si     (7-16)

(3) The negative entropy generation must be coupled into the system in such a way that the resultant work done is directed toward restoration of the system from disintegration that occurs naturally and is described by the second law of thermodynamics; i.e.,

       - Se = Si        (7-17)

where S_e and S_i refer not only to the magnitude of entropy change but also to the specific changes that occur in the system associated with this change in entropy. The coupling must produce not just any kind of ordering but the specific kind required by the system.

Concept (1) merely states that the overall entropy must increase for any real, i.e., irreversible process. With respect to concept 2, the terms S_e and S_i in equations 7-16 and 7-11 are described respectively as "entropy flux due to energy flow through the system and entropy production inside the system due to irreversible processes." Energy flow is described as a force that maintains a system far from equilibrium. No correlation between these concepts and the familiar equations of classical thermodynamics is given. Concept (3) appears only to state in a qualitative way that the chemical changes taking place in living things must maintain the order and complexity of the cell structures of living things.

Perhaps I am missing something, but, at least so far as Chapter 7 is concerned, there seems to be no basis for achieving the goal of reassessing current theories.