For thousands of years people speculated on the nature of the sun, moon, and stars and their relation to the earth. They developed all kinds of explanations, but no real information. Eventually some curious persons took a different approach, based on careful observation.

They noted the shift of elevation of the pole star with latitude and the fact that, at a distance, only the sails, not the hull of a ship could be seen. Could it be the earth was round? If so, how big around? Now here comes the scientific part: it occurred to a Greek named Eratosthenes in the third century b.c. that if the world was round, you could measure the circumference with a stick, a protractor, and a herd of camels. Except for using miles instead of stadia, this is exactly how he did it:

Eratosthenes knew that on the day of the summer solstice, at high noon, the sun shone directly down a vertical well in Aswan, Egypt without casting a shadow. On that same day at high noon a vertical stick in Alexandria would cast a shadow. On mulling it over, he concluded that the angle of the shadow would have to be equal to the angle of latitude difference between the two locations.

In order to determine the circumference of the earth, however, it would be necessary to know the north-south distance between the stick in Alexandria and the well in Aswan. As it turned out there was a camel herder trade route between the two locations. In questioning the camel herders, he determined the number of days necessary to travel from Aswan to Alexandria. Next step: find out how many miles a day a camel herd travels. Multiply one by the other, and you have the distance in miles between Aswan and Alexandria! Since Alexandria is essentially due north of Aswan, this distance is a equal to the required north-south distance.

Here is how he made the calculation:

Shadow angle: 7 degrees
Distance along the north-south line: 486 miles
Number of degrees in a circle: 360
486 miles x 360 / 7 = 25,000 miles circumference

The calculated diameter of the earth is calculated by dividing the circumference by = 3.14:

25,000 / 3.14 = 8000 miles

But wait! There's more! How about the diameter of the moon and its distance? With a little thought, we can figure that out, too! Here's a way of doing it:

During a lunar eclipse, the shadow of the earth on the moon indicates that the moon's diameter is about one-fourth that of earth, so we can estimate it at approximately 2000 miles.

The next step is to determinethe angle of the moon's disk in degrees. Get a smooth straight board at least 12 inches long. Hold one end up to your eye and sight along the board so that the other end just covers one-half of the disk of a full moon (cuts the moon in half). Mark the far end of the board at each edge of the moon's disk. This a little tricky, but it can be done. Draw lines from the point on the board corresponding to your "eye" position to each mark at the "moon" end of the board. This will form a narrow angle with the apex at the "eye" end. The angle can be measured with a protractor.

Assuming the ancients did not have a protractor, the angle can still be determined by creating a 30 degree angle with a compass and ruler, using the principles of plane geometry. Count the number of "moon" angles that will fit into the 30 degree angle. Since there are twelve 30 degree angles in a circle, multiply by 12 to obtain the number of moon images to complete a full circle.

Assume that we have determined that the moon's disk is close to 1/2 degree. Since there are 360 degrees in a full circle, the circle of the moon's orbit would contain 2 x 360 moons of diameter = 2000 miles. Therefore the circumference of the moon's orbit is equal to 2000 x 2 x 360 miles, which is equal to 1,440,000 miles. Dividing this figure by 2, we get the distance to the moon = 229,000 miles. (Note that this figure represents the distance to moon from the earth's surface, not from its center.)

In this and subsequent calculations, for simplicity we are assuming that the moon's orbit is a perfect circle. In fact, it is not a circle, but an ellipse. Also the measuring techniques are relatively crude. Therefore the calculated values, although reasonably close to the true values, will not be exact. The purpose here is to demonstrate how significant scientific data can be obtained by some very simple procedures.

Let's press on and figure out to see what else we can determine! Look at the moon just at sunset: when you see a half disk you'll notice that the moon is practically at right angles to the sun. Therefore the sun must be a LOT further away from us than the moon. If it weren't you would see more than just a half disk. Since the sun and moon appear in the sky at about the same size in degrees, we can conclude that the sun must be much larger than the moon.

Watch where the sun rises and sets during the year. You'll discover that in our northern hemisphere in June it rises north of east, swings around to the south, then sets north of west. In December, it rises south of east, swings around to the south, and sets south of west, taking a much shorter path. This, of course, explains why the days are shorter in winter than summer. In the spring and fall it rises at a point due east and sets at a point due west on the horizon. All of these trajectories are parallel to each other.

At the equator the sun rises and sets straight up. However in June it rises 23.5 degrees north of east and sets 23.5 degrees north of west. In December it rises 23.5 degrees south of east and sets 23.5 degrees south of east. From this, with a little thought, we can conclude that the axis of the earth's rotation is tipped 23.5 degrees.

So here is what we determined, using essentially no instrumentation:

Diameter of earth: 8000 miles
Diameter of moon: 2000 miles
Distance to moon: 229,000 miles
Inclination of earth's axis of rotation: 23.5 degrees.
Distance to the sun: much further away than the moon.
Size of sun: much larger than the moon.

Well, that's pretty good for starters, but now let's get just a little bit more technical and calculate the mass ("weight") of the earth, using 18th century technology:

Formula for the gravitational attraction F between two bodies, M and m, developed by Isaac Newton:

F = GMm / R² . . . . . . (1)

where:
G = universal gravitational constant, first measured by Cavendish in 1798
M = mass of earth
m = mass of moon
R = distance between center of earth and center of moon.

The value of G, the universal gravitational constant, was determined by Cavendish using the apparatus shown here:

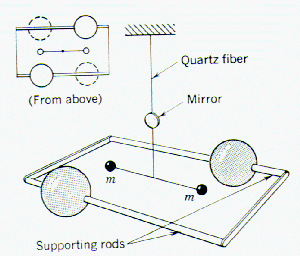
There is a gravitational attraction between the large lead balls M and the small balls m. This results in a slight twisting of the quartz fiber. When the large lead balls are shifted as shown in the upper left of the illustration, the direction of twist is reversed. This movement is amplified and measured by the deflection of a beam of light reflected from the mirror and projected on a ruled scale some distance away. The force corresponding to the twisting of the quartz fiber was previously calibrated using light weights.

Newton's second law of motion is expressed by the equation:

F = ma . . . . . .(2)

where:
F = gravitational force between earth and moon
m = mass of moon
a = acceleration

There are two kinds of acceleration. The first is a change in speed, for example going from 0 to 60 mph in 15 seconds. The second kind of acceleration involves a change in the direction of motion. Because the moon's path as it circles the earth is constantly changing in direction instead of continuing in a straight line, it is undergoing this second kind of acceleration, known as vector acceleration. The formula for vector acceleration, developed by Isaac Newton in the 17th century, is:

a = V² / R . . . . . .(3)

where:
a = acceleration
V = velocity of the moon in its orbit
R = radius of moon's orbit = distance of the moon from the earth

Combining equations (2) and (3) we have:
F = mV² / R . . . . . . (4)

Combining equations (1) and (4):

GMm / R² = mV² / R

Simplifying and rearranging, we have:

M = RV² / G . . . . . . (5)

The values for R, V, and G are:

G = 6.67 x 10^-11 meters³/kg.sec²
R = (229,000 + 4000)x 1,609 meters, center to center.
(the radius of earth, 4000 miles is added to the distance to convert to center to center)
(the factor 1,609 converts miles to meters)
R = 3.75 x 10⁸ meters

The moon makes a complete circle around the earth in 27.3 days. Because of the earth's revolution around the sun, the synodic "calendar" time from full moon to full moon is longer, 29.5 days. This is because the earth has to rotate a little more than 360 degrees each day to "catch up" to the sun. This means that the moon has to revolve around the earth more than 360 degrees in order to reappear in the same place in the night sky at the same time of the night. The extra time required for the moon to appear in the same place in the sky can be calculated as follows:

extra movement of the earth along its orbit = 360 / 12 months = 30 degrees/average month
fraction of moon's orbit to be made up = 30 / 360 = .0833
days of moon's orbit needed to catch up = (27.3)x(0.0833) = 2.2 days
days per calendar month = 27.3 + 2.2 = 29.5

Therefore:
V = 2R / (days per moon's orbit)
since R = 3.75 x 10⁸ meters
V = 2 x 3.75 x 10⁸) x 3.14 / 27.3 meters/day
V = 2 x 3.75 x 10⁸ x 3.14 / (27.3 x 24 x 3600) meters/sec
V = 1000 meters/sec

Plugging in the above values in equation (5), we get:

M = 3.75 x [(1000)² / 6.67] x 10¹⁹,
or
M = 5.6 x 10²⁴ kilograms,
or
M = 5.6 x 10²¹ metric tons

The accepted "correct" value is 5.97 x 10²¹ metric tons.